Радиус вписанной окружности в правильный многоугольник, формула
|
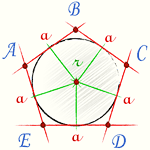
Правильный многоугольник — это многоугольник с равными сторонами и углами. Угол между двумя соседними вершинами правильного n-угольника равен:
\[AOB = α = \frac{360°}{n}\]
|
 |
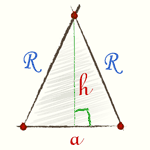 |
Построим треугольник AOB отдельно. Об этом треугольнике мы знаем: он равнобедренный, и высота этого треугольника это радиус вписанной окружности правильного многоугольника. Также нам известна длина основания a этого треугольника — которое является стороной исходного правильного многоугольника. |
Также известен угол между бедрами — по формуле (1). Опустим высоту на основание и рассмотрим получившийся прямоугольный треугольник. При помощи тригонометрических функций острого угла получим:
\[\tg\bigg(\frac{360°}{2n}\bigg) = \frac{a}{2r}\]
отсюда получим формулу радиуса вписанной окружности правильного многоугольника:
\[r = \frac{a}{2 \tg(\frac{360°}{2n})}\]
(a - сторонa правильного многоугольника; n - число сторон правильного многоугольника; r - радиус вписанной окружности правильного многоугольника)Вычислить, найти радиус вписанной окружности в правильный многоугольник по формуле (3)
Радиус вписанной окружности в правильный многоугольник |
стр. 256 |
|---|
