Точки, прямые, отрезки

точки и прямая

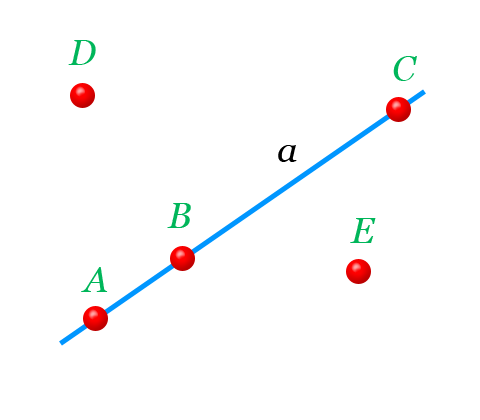
Точка это некоторое положение в пространстве, двухмерном или трехмерном. Точке присущи некоторые координаты. Чтобы обозначить точку на чертеже, используют закрашенный кружок диаметром 1-2 мимллиметра. Обозначают точки большими латинскими буквами - например A, B, C.

Изображение прямой на чертеже

Прямая является бесконечной линией. У нее нет начала и нет конца. Для того чтобы изобразить часть прямой необходимо приложить линейку к листу бумаги и провести линию вдоль нее карандашом. Чтобы обозначить прямую на чертеже используют маленькие латинские буквы — например a, b, c.

Геометрическое место точек

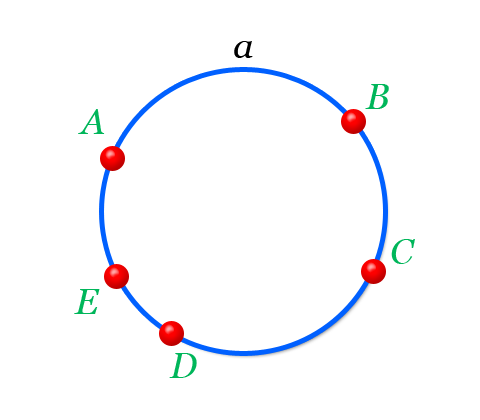
Точки расположенные в пространстве можно соединить каким либо образом, тогда говорят о некотором геометрическом месте точек которые они образуют. Например точки, соединенные плавной дугой окружности — образуют геометрическое место — окружность. Также говорят, что эти точки принадлежат некоторой линии или плоскости — в примере выше — окружности.

Аксиома прямой

Точки и прямые связаны и о них можно сказать следующее:

Прямую a можно провести через любые две точки A и B, но при этом она — прямая, будет единственно возможной прямой которой принадлежат эти две точки.

Пересекающиеся прямые

Пересекающиеся и параллельные прямые

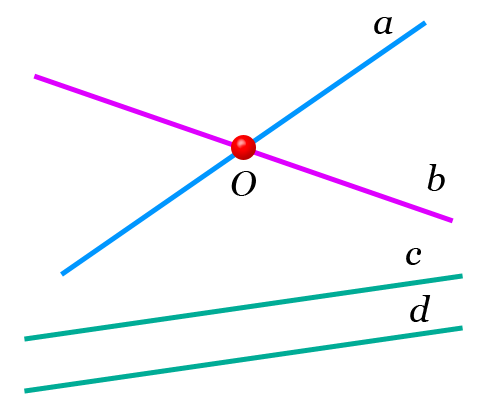
Если две прямые имеют одну общую точку, то говорят, что они пересекаются. Согласно предыдущего утверждения две разные прямые не могут иметь более одной общей точки.

На плоскости если прямые не имеют общей точки — то они параллельны. Для прямых расположенных в пространстве не на одной плоскости это утверждение неверно.

отрезок

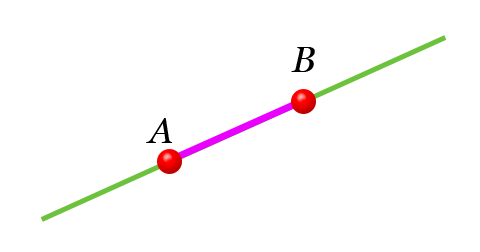
Если указать на прямой две точки, то линию соединяющую эти две точки и называют отрезок. Концы отрезка — это и есть эти две точки. Отрезок обозначается буквами обоих точек — например AB.