Упругое соударение
Соударение — это столкновение двух тел. При соприкосновении тела обмениваются энергией и импульсом. После соударения они двигаются со скоростями, которые отличаются по направлению и величине от их скоростей до столкновения.
При лобовом центральном соударении центры масс обоих тел двигаются вдоль одной линии. Силы взаимодействия, возникающие при соударении, параллельны направлению движения. Если применить к такой системе двух тел закон сохранения импульса, то полный импульс системы будет равен алгебраической сумме импульсов обоих тел.
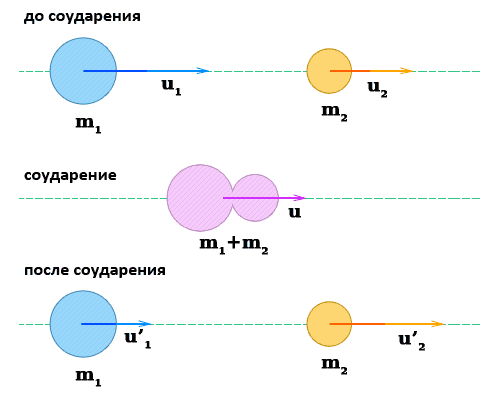
При упругом соударении на протяжении кратковременного соприкосновения тела двигаются с общей скоростью, затем они разлетаются и продолжают двигаться с разными скоростями.
Если
| m1 | масса первого тела, | кг |
|---|---|---|
| m2 | масса второго тела, | кг |
| u1 | скорость первого тела до соударения, | метр/секунда |
| u2 | масса второго тела до соударения, | метр/секунда |
| u`1 | скорость первого тела после соударения, | метр/секунда |
| u`2 | масса второго тела после соударения, | метр/секунда |
то из закона сохранения импульса следует
или
Из закона сохранения энергии получаем
или
подставив формулу разность квадратов получим
воспользовавшись законом сохранения импульса, находим
Сумма скоростей до и после соударения одинакова при любом соударении тел.
Из формулы (6) следует
Подставив эти выражения в видоизмененный закон сохранения импульса, получим
откуда, разрешив относительно u`1 и u`2 найдем
При противоположном направлении; движения скорость считается отрицательной.
Поскольку полная энергия до и после соударения остается неизменной, после столкновения тела приобретают свою первоначальную форму, возникающие в момент соударения деформации исчезают.
Упругое соударение, вычислить скорости тел после упругого соударения
Упругое соударение |
стр. 477 |
|---|
