Высота тетраэдра, формула
 |
Высота тетраэдра — равна корню квадратному из двух третьих, помноженному на длину ребра тетраэдра
\[ h = \sqrt{\frac{2}{3}} a \]
(h - высота тетраэдра, a - ребро тетраэдра)
|
Вывод формулы высоты тетраэдра
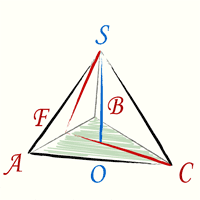
Чтобы получить формулу высоты тетраэдра необходимо произвести дополнительные геометрические построения. На рисунке красные линии CF и FS — это высоты соответствующих правильных треугольников ABC и ABS:
\[CF = FS = \frac{\sqrt{3}}{2}a ; CS = a \]
Теперь в треугольнике CFS известны все стороны. Высота тетраэдра, как видно из геометрических построений — это высота треугольника CFS. Подставив стороны треугольника в формулу и произведя простые сокращения (используем формулу разность квадратов) получим формулу (1).
\[p = \frac{1}{2}(a + a\frac{\sqrt{3}}{2} + a\frac{\sqrt{3}}{2}) \]
\[p = \frac{1}{2} a (1 + \sqrt{3}) \]
\[h = 2 \frac{ \sqrt{p(p-a)(p-(a\frac{\sqrt{3}}{2}))(p-(a\frac{\sqrt{3}}{2}))}}{a\frac{\sqrt{3}}{2}}\]
\[h = 2 \frac{\sqrt{(\frac{a}{2})^4 (\sqrt{3}+1) (\sqrt{3}-1)}}{a\frac{\sqrt{3}}{2}} = \sqrt{\frac{2}{3}} a \]
Вычислить, найти высоту тетраэдра по формуле(1)
Высота тетраэдра |
стр. 283 |
|---|
