Сложение и вычитание дробей
Если знаменатели дробей одинаковы, то, чтобы сложить дроби, нужно сложить их числители, а чтобы вычесть дроби, нужно из числителя уменьшаемого вычесть числитель вычитаемого. Полученная сумма или разность будет числителем результата. Знаменатель остается прежним.
\[ \frac{5}{9} + \frac{7}{9} = \frac{12}{9} = 1 \frac{3}{9} = 1 \frac{1}{3} \]
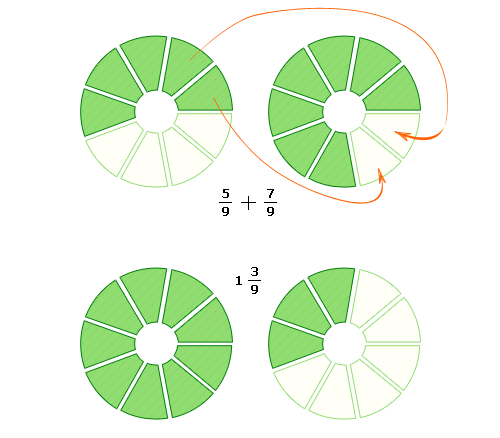
Сложение и вычитание дробей
Если знаменатели дробей различны, нужно предварительно привести дроби к общему знаменателю.
\[ \frac{5}{9} + \frac{7}{8} = \frac{40}{72} + \frac{63}{72} = \frac{103}{72} = 1 \frac{31}{72} \]
Если складываются смешанные числа, то отдельно находят сумму целых и сумму дробных частей.
\[ 3\frac{5}{9} + 4\frac{7}{8} = \\ \space \\ = (3+4) + (\frac{40}{72} + \frac{63}{72}) = \\ \space \\ = 7 + \frac{103}{72} = 8 \frac{31}{72} \]
При вычитании смешанных чисел дробная часть вычитаемого может оказаться больше дробной части уменьшаемого. Тогда в уменьшаемом «занимается» единица и обращается в неправильную дробь.
\[ 5\frac{5}{9} - 3\frac{7}{8} = \\ \space \\ = 5\frac{40}{72} - 3\frac{63}{72} = \\ \space \\ = 4\frac{112}{72} - 3\frac{63}{72} = 1\frac{49}{72} \]
Произвести сложение дробей
Произвести вычитание дробей
Сложение и вычитание дробей |
стр. 30 |
|---|
