Сложение колебаний одинаковой частоты одного направления
При наложении двух гармонических колебаний, происходящих в одном направлении с одинаковой частотой, возникает гармоническое колебание с той же частотой, а его амплитуда зависит от амплитуд и начальных фаз отдельных колебаний. Результирующее отклонение в каждый момент времени равно алгебраической сумме составляющих отклонений.
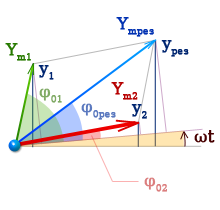
Если
| Ym1 | Амплитуда колебаний 1, | метр |
|---|---|---|
| у1 | Отклонение колебаний 1, | метр |
| φ01 | начальная фаза колебаний 1, | радиан |
| Ym2 | Амплитуда колебаний 2, | метр |
| у2 | Отклонение колебаний 2, | метр |
| φ02 | начальная фаза колебаний 2, | радиан |
| ω | частота колебаний, | радиан/сек |
| t | продолжительность колебаний, | сек |
| Ymрез | Амплитуда результирующих колебаний, | метр |
| урез | Отклонение результирующих колебаний, | метр |
| φ0рез | начальная фаза результирующих колебаний, | радиан |
то
Многократного применения теорему сложения, получаем
при этом
и
На рисунке амплитуды представлены векторами. Их направления соответствуют начальным фазам. В течение времени t они поворачиваются на один и тот же угол ωt, поскольку колебания имеют одинаковую частоту. Представление колебаний с помощью вращающихся векторов называется векторной диаграммой. Оно позволяет находить амплитуду и отклонение, не прибегая к математическим выкладкам.
В частном случае равных амплитуд (Ym1 = Ym2) выражения (3) и (4) упрощаются:
и
Для разности начальных фаз ∆φ = 0 или π получаем следующие частные случаи:
| Условия | Результат | |
|---|---|---|
| Ym1 = Ym2 | ∆φ = 0 | Отклонения удваиваются |
| Ym1 ≠ Ym2 | ∆φ = 0 | Отклонения суммируются |
| Ym1 = Ym2 | ∆φ = π | Оба колебания взаимно уничтожаются |
| Ym1 ≠ Ym2 | ∆φ = π | Отклонения вычитаются |
Обратите внимание:
Сложение колебаний одинаковой частоты |
стр. 561 |
|---|
