Равенство векторов
Два (ненулевых) вектора a и b равны, если они равнонаправлены и имеют один и тот же модуль. Все нулевые векторы считаются равными. Во всех остальных случаях векторы не равны.
Следующая запись выражает, что векторы a и b равны.
\[ \vector{a} = \vector{b} \]
Запись
\[ \vector{a} \not = \vector{b} \]
выражает что векторы не равны.
В этом случае
\[ \lvert \vector{a} \rvert = \lvert \vector{b} \rvert \]
модули (длины) векторов равны, при этом сами векторы могут равняться, а могут и не равняться друг другу.
Примеры равенства и неравенства векторов
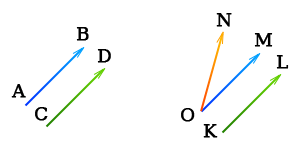
равенство векторов
Векторы AB и СD равны.
Векторы ON и OM не равны. Их модули (длины) одинаковы, однако их направления различны. Векторы ON и KL тоже не равны. А векторы OM и KL равны.
Два вектора будут равны только в том случае, когда их можно совместить без поворота.
Равенство векторов |
стр. 168 |
|---|
