Сумма нескольких векторов
Сумма нескольких векторов а1, а2, а3, … , аn, это вектор, получающийся после ряда последовательных сложений: к вектору а1 прибавляется вектор а2, к полученному вектору прибавляется вектор а3 и т.д.
Из определения вытекает такое построение

Правило многоугольника или правило цепи
Из произвольного начала О строим вектор ОА1 = а1, из точки А1, как из начала, строим вектор А1А2 = а2, из точки А2 строим вектор А2А3 = а3 и т.д. Вектор ОАn (на рисунке n = 6) есть сумма векторов а1, а2, … , аn.
Сумма векторов а1, а2, а3, а4, а5, а6 обозначается
Свойство сочетательности
Слагаемые векторы можно группировать как угодно.
Так, если найти сначала сумму векторов
и к ней прибавить вектор а1 (ОА1), то получим то же вектор:
Правило параллелепипеда
Если три вектора а, b, с после приведения к общему началу не лежат в одной плоскости, то сумму а+b+c можно найти таким построением:
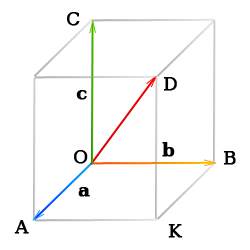
Из любого начала О строим векторы ОА = а, ОВ = b, ОС = с, на отрезках ОА, ОВ, ОС, как на ребрах, строим параллелепипед. Вектор диагонали OD есть сумма векторов a, b, и c (так как ОА = а, АК = ОВ = b, KD = OC = c и OD = OA + AK + KD).
К векторам, которые (после приведения к общему началу) лежат в одной плоскости, это построение неприменимо.
Сумма нескольких векторов |
стр. 172 |
|---|
