Сложение векторов, Сумма векторов
Правило треугольника
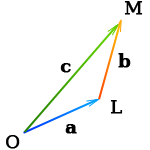
Сумма векторов a и b это третий вектор с, получаемый следующим построением: из произвольного начала О строим вектор OL, равный а; из точки L, как из начала строим вектор LM, равный b. Вектор с = ОМ есть сумма векторов a и b («правило треугольника»).
При сложении векторов справедливы неравенства
Эти неравенства показывают, что сторона OM треугольника OML меньше суммы и больше разности двух других сторон.
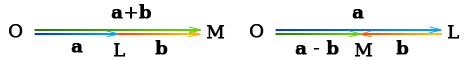
В формуле (1) знак равенства имеет место только для равнонаправленных векторов, в формуле (2) – только для противоположного направленных векторов.
Сумма противоположных векторов
Из определения следует, что сумма противоположных векторов равна нуль-вектору.
Свойство переместительности
От перестановки слагаемых сумма не изменяется.
Правило параллелограмма
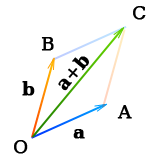
Если слагаемые a и b не коллинеарны, то сумму a + b можно найти следующим построением:
из любого начала О строим векторы ОА = а и ОВ = b; на отрезках ОА, ОВ строим параллелограмм ОАСВ. Вектор диагонали ОС = с есть сумма векторов a и b (так как АС = OB = b и ОС = ОА + АС).
К коллинеарным векторам это построение неприменимо.
Определение сложения векторов установлено в соответствии с физическими законами сложения векторных величин (например, сил, приложенных к материальной точке).
Сложение векторов, Сумма векторов |
стр. 171 |
|---|
