Уравнение траектории тела, брошенного горизонтально
Если построить траекторию движения тела, брошенного горизонтально, в системе координат xy, приняв за начало отсчета координат точку бросания, а направление оси ординат совпадающим с направлением вектора ускорения свободного падения, то координаты каждой точки P траектории представляют собой перемещение тела в горизонтальном направлении (движение с постоянной скоростью u0) и в вертикальном направлении (равномерно ускоренное движение с ускорением g)
Здесь:
x, y — координаты тела,
u0 — начальная скорость тела (м/с),
g — ускорение свободного падения 9.81 (м/c2),
t — время движения (c)
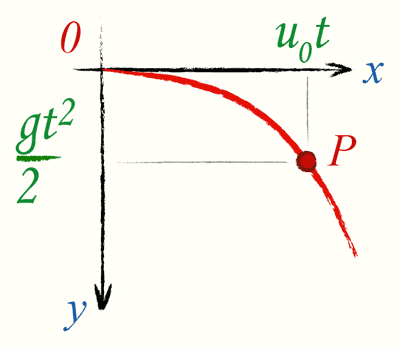
Уравнение траектории тела, брошенного горизонтально
Уравнение траектории тела, брошенного горизонтально выглядит следующим образом:
Так как ускорение свободного падения g и начальная скорость тела u0 — постоянные величины, то координата y пропорциональна квадрату x, т.е. траектория движения представляет собой параболу, вершина которой находится в начальной точке движения.
Сопротивление воздуха в формулах не учитывается.
Расчитать точки траектории тела, брошенного горизонтально по формуле (2)
Построить график траектории тела, брошенного горизонтально по формуле (2)
Уравнение траектории тела, брошенного горизонтально |
стр. 412 |
|---|
