Гиперболический параболоид, уравнение гиперболического параболоида
уравнение поверхности второго порядка
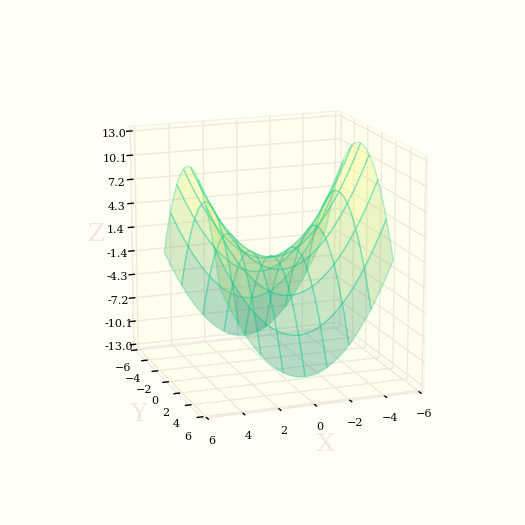
Поверхность, представляемая уравнением
\[ z = \frac{x^2}{2p} - \frac{y^2}{2q} \]
при (p > 0, q > 0), носит название гиперболический параболоид.
Сечения плоскостями XOZ и YOZ (главные сечения — это параболы).
\[ x^2 = 2pz \]
\[ y^2 = -2qz \]
Параболы (2 и 3) обращены вогнутостью в противоположные стороны. Поверхность имеет седлообразный вид.
Гиперболический параболоид не имеет центра. Он симметричен относительно плоскостей XOZ и YOZ и относительно оси OZ. Прямая OZ называется осью гиперболического параболоида.
Гиперболический параболоид не является поверхностью вращения.
Построить поверхность гиперболического параболоида в 3D
Гиперболический параболоид, уравнение гиперболического параболоида |
стр. 159 |
|---|
