Однополостный гиперболоид, Уравнение однополостного гиперболоида
уравнение поверхности второго порядка
Однополостный гиперболоид с центром в начале координат представлен уравнением второй степени.
\[ \frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=1 \]
Наименование гиперболоид происходит от того, что среди сечений этой поверхности есть гиперболы. Эти сечения предсталяются уравнениями:
\[ \frac{y^2}{b^2}-\frac{z^2}{c^2}=1 \]
и
\[ \frac{x^2}{a^2}-\frac{z^2}{c^2}=1 \]
Название Однополостный подчеркивает, что поверхность не разорвана на две полости, а представляет собой одну сплошную бесконечную трубку, вытянутую вдоль оси OZ.
Построить поверхность однополостного гиперболоида в 3D
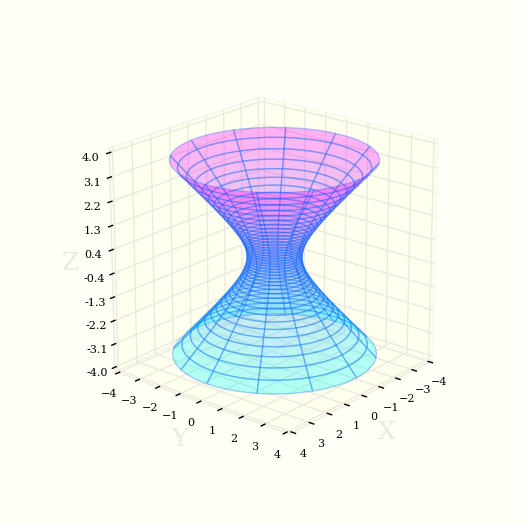
Однополостный гиперболоид, Уравнение однополостного гиперболоида |
стр. 156 |
|---|
