Деление отрезка в данном соотношении, формула
Деление отрезка в данном соотношении
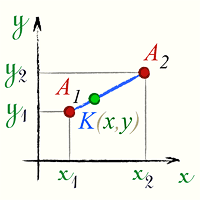
Даны точки A1(x1;y1) и A2(x2;y2). Требуется найти координаты точки K(x;y), делящей отрезок A1A2, в данном отношении.
\[ \frac{A_1 K}{K A_2} = \frac{m}{n} = λ \]
Координаты точки делящей отрезок в данном соотношении находятся по формулам:
\[
x = \frac{n x_2 + m x_2}{m + n} = \frac{x_1 + λ x_2}{1 + λ} \\ \medspace \\
y = \frac{n y_2 + m y_2}{m + n} = \frac{y_1 + λ y_2}{1 + λ}
\]
Выражение "точка K делит отрезок A1A2 в отношении m:n" означает, что отношение m:n равно отношению отрезков A1K:KA2, взятых именно в этом порядке, а не в обратном.
Если отношение m:n имеет отрицательный знак — значит точка K делит отрезок A1A2 внешним образом, т.е. находится вне этого отрезка и лежит на его продолжении.
Построить деление отрезка в данном соотношении на координатной плоскости
найти координаты точки делящей отрезок в данном соотношении по формуле (2)
Деление отрезка в данном соотношении |
стр. 139 |
|---|
