Формулы и расчеты онлайн - Fxyz.ru

← Назад	Вперед →

Угол между двумя прямыми

Пусть две неперпендикулярные прямые L1, L2 (взятые в данном порядке) представляются уравнениями

\[ \begin{cases} y = a_{1} x + b_{1} \\ y = a_{2} x + b_{2} \end{cases} \]

Тогда угол между двумя прямыми найдется по формуле

\[ \tg(θ) = \frac{a_{2} - a_{1}}{1 + a_{1} a_{2}} \]

Угол между двумя прямыми

Если прямые L1 и L2 перпендикулярны (θ = ± 90°)

то выражение стоящее в знаменателе, обращается в нуль

\[ 1 + a_{1} a_{2} = 0 \]

и частное перестает существовать. Одновременно перестает существовать («обращается в бесконечность») tg(θ). Формула (2), понимаемая буквально, теряет смысл, но в этом случае ее нужно понимать условно. Именно, всякий раз, как в знаменателе появляется нуль, угол θ надо считать равным ±90° (как поворот на +90°, так и поворот на -90° совмещает любую из перпендикулярных прямых с другой).

Если хотя бы одна из прямых L1, L2 (или обе) параллельна оси OY

то формула (2) вовсе неприменима, ибо тогда одну из прямых (или обе) нельзя представить уравнением вида (1).

В этом случае угол θ определяется следующим образом:

а) когда прямая L2 параллельная оси OY, а L1 не параллельна, применяем формулу

\[ \tg(θ) = \frac{1}{a_{1}} \]

б) когда прямая L1 параллельна оси OY, а L2 не параллельна, применяем формулу

\[ \tg(θ) = -\frac{1}{a_{1}} \]

в) когда обе прямые параллельны оси OY, они параллельны и между собой, так что

\[ \tg(θ) = 0 \]

Найти угол между двумя прямыми по формуле (2)

Угол между двумя прямыми, заданными уравнениями

\[ \begin{cases} А_{1} x + В_{1} y + С_{1} = 0 \\ А_{2} x + В_{2} y + С_{2} = 0 \end{cases} \]

можно найти по формуле

\[ \tg(θ) = \frac{A_{1} B_{2} - A_{2} B_{1}}{A_{1} A_{2} + B_{1} B_{2}} \]

При

\[ A_{1} A_{2} + B_{1} B_{2} = 0 \]

формула, понимаемая условно, дает

\[ θ = \plusmn 90° \]

Найти угол между двумя прямыми по формуле (9)

Примеры

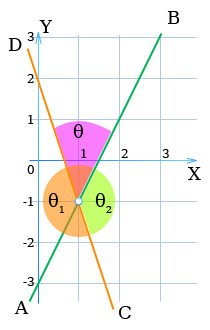
Пример 1.

Найти угол между двумя прямыми

\[ \begin{cases} y = 2x - 3 \\ y = -3x + 2 \end{cases} \]

Здесь

\[ a_1 = 2, a_2 = -3 \]

По формуле (2) находим:

\[ \tg(θ) = \frac{-3-2}{1 + 2 \cdot (-3)} = 1 \]

Отсюда

\[ θ = \pm 45° \]

Это значит, что прямая АВ

\[ y = 2x – 3 \]

повернутая на угол +45° около точки пересечения М(1; -1) данных прямых, совместится с прямой CD

\[ y = -3x + 2 \]

Можно взять также

\[ θ = 180° + 45° = 225° \]

\[ θ = -180° + 45° = -135° \]

и т. д.

Эти углы обозначены θ₁, θ₂ на рисунке

Пример 2.

Найти угол между двумя прямыми

\[ \begin{cases} y = -3x + 2 \\ y = 2x - 3 \end{cases} \]

Прямые здесь те же, что и в примере 1, но теперь прямая CD — первая, а прямая AB — вторая. Формула (2) дает

\[ \tg(θ) = - 1 \]

т.е.

\[ θ = -45° \]

(или θ = 135°, или θ = -225° и т. д.).

На этот угол надо повернуть прямую CD до совмещения с AB.

Пример 3.

Найти угол между прямыми

\[ \begin{cases} y = 2x - 3 \\ y = -\frac{1}{2}x + 7 \end{cases} \]

\[ a_1 = 2, a_2 = -\frac{1}{2} \]

Если предварительно поставить вопрос: перпендикулярны ли эти прямые, то по признаку перпендикулярности двух прямых получим утвердительный ответ,

так что и без формулы (2) получаем

\[ θ = ± 90° \]

То же дает и формула (2). Мы получаем:

\[ \tg(θ) = \frac{-\frac{1}{2}-2}{1 + (-\frac{1}{2}) \cdot 2} = \frac{-1}{0} \]

Угол между двумя прямыми	стр. 149

A₁	B₁
A₂	B₂


e	π	g	C
sin	cos	tan	√	exp
asin	acos	atan	lg	ln
7	8	9	(	)
4	5	6	×	÷
1	2	3	+	-
0	.	=

Угол между двумя прямыми

Найти угол между двумя прямыми по формуле (2)

Угол между двумя прямыми, заданными уравнениями

Найти угол между двумя прямыми по формуле (9)

Примеры

Угол между двумя прямыми

См. также

Разделы

Калькулятор

Дополнительно