Площадь треугольника через координаты
Площадь треугольника через координаты
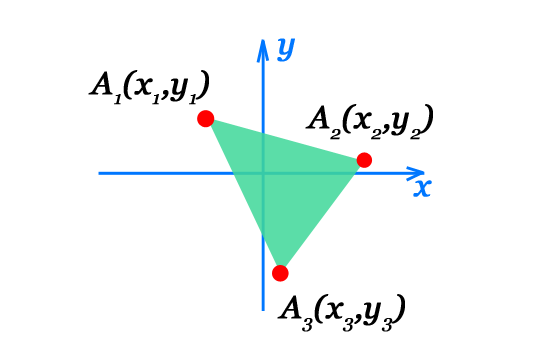
Если вершины треугольника заданы, как точки в прямоугольной декартовой системе координат: A1(x1,y1), A2(x2,y2), A3(x3,y3), то площадь такого треугольника можно вычислить по формуле определителя второго порядка:
\[ S = \pm \frac{1}{2}
\begin{vmatrix}
x_1-x_3 & y_1-y_3 \\
x_2-x_3 & y_2-y_3
\end{vmatrix}
\]
Поскольку площадь должна быть положительной величиной, то перед определителем стоит знак плюс-минус. Если определитель отрицательный то берем знак минус, что в итоге даст плюс. Если определитель положительный то берем знак плюс. Или просто возьмем абсолютное значение определителя поделенное на два.
Пример нахождения площади треугольника через координаты
Пусть заданы вершины A1(3,2), A2(7,5), A3(0,0).
Пример нахождения площади треугольника через координаты
Получим формулу:
\[ S = \pm \frac{1}{2}
\begin{vmatrix}
3-0 & 2-0 \\
7-0 & 5-0
\end{vmatrix}
\]
\[ S = \pm \frac{1}{2}
\begin{vmatrix}
3 & 2 \\
7 & 5
\end{vmatrix}
\]
\[ S = \frac{1}{2} (15-14) = \frac{1}{2} \]
Вычислить площадь треугольника через координаты его вершин онлайн
Площадь треугольника через координаты |
стр. 150 |
|---|
