Частота биений, формула
Период биений
Период биений Тб — это промежуток между соседними моментами времени, в которые амплитуда обращается в нуль, а фаза изменяется на π.
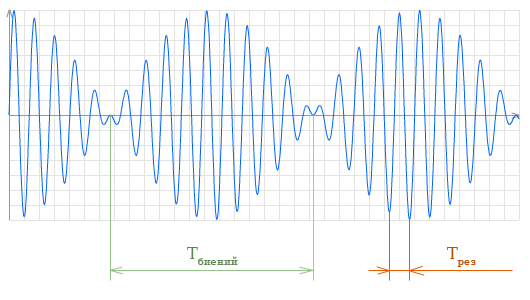
Частота биений, Период биений, Результирующая частота
Поскольку при аргументе, равном π/2, 3π/2 …, косинус обращается в нуль, имеем:
\[ \frac{ω_{1}-ω_{2}}{2} T_{б} = π \]
Отсюда при
\[ ω = 2πf \]
следует
\[ \frac{2πf_{1}-2πf_{2}}{2} = π f_{б} \]
Решая это уравнение относительно частоты биений, получаем
\[ f_{б} = f_{1} - f_{2} \]
Частота биений
Частота биений есть отношение числа минимумов амплитуды ко времени. Частота биений определяется как разность частот составляющих колебаний.
Из (4) при
\[ Т_{б} = \frac{ 1 }{ f_{б}} \]
получаем
\[ Т_{б} = \frac{ T_1 T_2 }{ T_2 - T_1 } \]
Частота результирующих колебаний получается из формулы результирующего отклонения биений [2]
\[ f_{рез} = \frac{ f_1 + f_2 }{ 2 } = \average{f} \]
Отсюда находим период результирующих колебаний Трез = 1/fрез
\[ Т_{рез} = 2 \frac{ T_1 T_2 }{ T_1 + T_2 } \]
Вычислить, найти частоту биенй по формуле (4)
Частота биений |
стр. 564 |
|---|
