Работа в гравитационном поле, формула

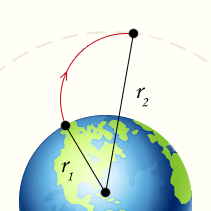
Если тело перемещается в гравитационном поле на значительное расстояние, то совершаемую против сил гравитационного притяжения работу (например, работу для вывода ракеты в космос) нельзя вычислить по формуле W=G·h, потому, что сила тяжести G обратно пропорциональна расстоянию между центрами масс.

Работа, совершаемая при перемещении тела вдоль радиуса в гравитационном поле, определяется как интеграл

См. Таблицу интегралов

Здесь:
W — работа против гравитационной силы (Джоуль),
G — гравитационная сила, с которой два тела притягиваются друг к другу (Ньютон),
m_a — масса первого тела (кг),
m_b — масса второго тела (кг),
r — расстояние между центрами масс тел (метр),
r₁ — начальное расстояние между центрами масс тел (метр),
r₂ — конечное расстояние между центрами масс тел (метр),
γ — гравитационная постоянная 6.67 · 10^-11 (м³/(кг · сек²)),

Величина работы W не зависит от формы пути от точки r₁ к r₂, так как в формулу входят только радиальные составляющие dr перемещения, совпадающие с направлением силы притяжения.

формула (3) справедлива в случае любых небесных тел.

Вычислить, найти работу в гравитационном поле по формуле (3)