Равномерно ускоренное движение по окружности без начальной угловой скорости
Тело начинает двигаться из состояния покоя, и его угловая скорость равномерно возрастает.
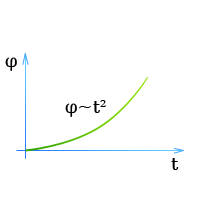
Если
ω — мгновенная угловая скорость тела в момент времени t,
α — угловое ускорение, постоянное в течение времени t,
φ — угловое перемещение тела за время t, (φ в радианах)
t — время,
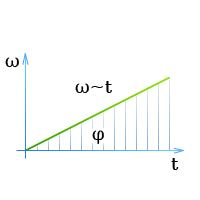
То, поскольку на графике скорости угловое перемещение равно площади треугольника, имеем
\[
φ = \frac{ωt}{2}
\]
Или по формуле (3)
\[
φ = \frac{αt^2}{2}
\]
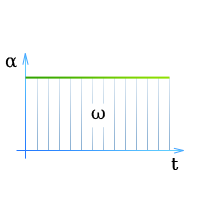Поскольку вращение тела начинается из состояния покоя, изменение угловой скорости Δω равно достигнутой в результате ускорения угловой скорости ω. Поэтому формула (6) принимает следующий вид:
\[
ω = αt
\]
\[
t = \frac{ω}{α}
\]
Подставляя этот результат в формулу (1), после перестановки получим
\[
ω = \sqrt{2αφ}
\]
Движение без начальной угловой скорости |
стр. 425 |
|---|
