Равномерно ускоренное движение по окружности с начальной угловой скоростью
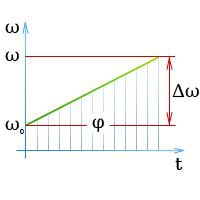Начальная скорость тела, равная ω0 в момент t = 0, изменяется равномерно на величину Δω.
(Угловое ускорение при этом постоянно.)
Если
ω0 — начальная угловая скорость,
ω — конечная угловая скорость,
φ — угловое перемещение тела за время t в радианах,
t — время,
α — угловое ускорение постоянное в течение времени t,
то, поскольку на графике скорости угловое перемещение соответствует площади трапеции под кривой скорости, имеем
\[
φ = \frac{ω_0 + ω}{2} t
\]
Так как площадь трапеции равна сумме площадей образующих ее треугольника и прямоугольника, получаем
\[
φ = ω_0 t + \frac{ω - ω_0}{2} t
\]
, откуда
\[
φ = ω_0 t + \frac{αt^2}{2}
\]
Далее из графика скорости следует
\[
ω = ω_0 + αt
\]
Разрешив уравнение (3) относительно t и подставив результат в (1) найдем
\[
φ = \frac{ω^2 - ω_0 ^2}{2α}
\]
После преобразования получаем выражение, не содержащее времени:
\[
ω = \sqrt{ω_0 ^2 + 2αφ}
\]
Движение с начальной скоростью |
стр. 426 |
|---|
