Равномерно ускоренное движение тела по окружности
Движение по окружности называется равномерно ускоренным, если
● угловое ускорение α = const, или
● угловая скорость ω пропорциональна времени t
 Если
Если
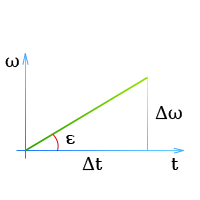
α — угловое ускорение,
Δω — изменение скорости вращения (увеличение или уменьшение),
Δt — время, за которое происходит это изменение угловой скорости,
то
Согласно этому выражению, угловое ускорение на графике скорости характеризуется тангенсом угла между касательной к кривой скорости и осью времени:
Постоянным угловым ускорением называется отношение изменения угловой скорости к продолжительности этого изменения.
Единица СИ углового ускорения:
Обратите внимание: угловое замедление отличается от углового ускорения только знаком (отрицательным)
● Угловое ускорение: α > 0
● Угловое замедление: α < 0
При движении тела по окружности с постоянным угловым ускорением следует различать два случая: движение с начальной угловой скоростью и без нее.
Вычислить найти угловое ускорение для равномерно ускоренного движения тела по окружности по формуле (1)
Равномерно ускоренное движение тела по окружности |
стр. 424 |
|---|
