Определитель третьего порядка, формула
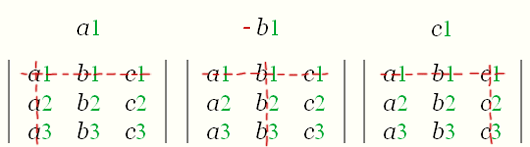Определитель третьего порядка
Определитель третьего порядка —
\[
\begin{vmatrix}
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2 \\
a_3 & b_3 & c_3
\end{vmatrix}
\]
есть сокращенное обозначение выражения
\[ \Delta = a_1 b_2 c_3 - a_1 b_3 c_2 + b_1 c_2 a_3 - \\ - b_1 c_3 a_2 + c_1 a_2 b_3 - c_1 a_3 b_2 \]
или выраженное через определители второго порядка
\[
a_{1}
\begin{vmatrix}
b_2 & c_2 \\
b_3 & c_3
\end{vmatrix}
-
b_{1}
\begin{vmatrix}
a_2 & c_2 \\
a_3 & c_3
\end{vmatrix}
+
c_{1}
\begin{vmatrix}
a_2 & b_2 \\
a_3 & b_3
\end{vmatrix}
\]
Определители второго порядка, входящие в выражение (3), составлены следующим образом. Вычеркнем из таблицы (1) ту строку, и тот столбец, где стоит a1. Остающийся определитель входит в (3) множителем при вычеркнутой букве a1. Аналогично получаются два других определителя формулы.
Средний определитель в формуле (3) имеет знак минус!
Вычислить, найти определитель третьего порядка по формуле (3)
Определитель третьего порядка |
стр. 143 |
|---|
