Математический маятник, формула
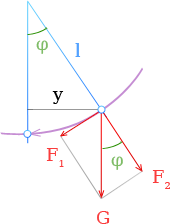
Математический маятник, представляющий собой точечную массу на невесомой нити, что нельзя реализовать в действительности. Однако, если масса нити пренебрежимо мала по сравнению с массой m тела и длина нити велика по сравнению с размерами тела, то с достаточной точностью выполняется формула (4). Математический маятник совершает гармонические колебания, если угол отклонения не превышает примерно 8º.
Если
| Т | период, длительность полного колебания, | секунда |
|---|---|---|
| l | длина маятника, расстояние от точки подвеса до центра масс, | метр |
| g | ускорение свободного падения на поверхности Земли 9,81 | метр / секунда2 |
то
\[
G = mg
\]
\[
\frac{F_{1}}{G} = \frac{y}{l}
\]
и, поскольку величину у при малом угле отклонения φ можно приравнять длине дуги, аналогично формуле Собственная частота колебаний [1] получаем
\[
D = \frac{F_{1}}{y} = \frac{G}{l} = \frac{mg}{l}
\]
Подстановка в Собственная частота колебаний [5] дает
\[
T = 2π \sqrt{\frac{ml}{mg}} = 2π \sqrt{\frac{l}{g}}
\]
Период Т не зависит от массы тела. В указанных пределах (φ < 8º) период не зависит от амплитуды.
Математический маятник - опыт
Математический маятник |
стр. 546 |
|---|
