Колебания пружины, формула
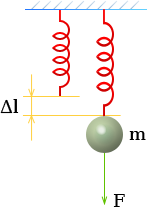
При колебаниях пружины восстанавливающая сила обусловлена ее упругостью. В определенных пределах, согласно закону Гука, вызванная деформацией сила пропорциональна величине деформации.
Поэтому упругие колебания являются гармоническими. В случае пружин величина жесткости обычно обозначается через k и именуется коэффициентом упругости пружины.
Если
| k | коэффициент упругости пружины, | Ньютон / метр |
|---|---|---|
| F | сила, вызывающая деформацию Δl, | Ньютон |
| Δl | удлинение, прогиб или другое изменение формы, | метр |
| ω | угловая частота, | радиан / секунда |
| f | линейная частота, | Герц |
| T | период, длительность полного колебания, | секунда |
| m | масса колебательной системы, обычно тела, укрепленного на пружине, | кг |
то
\[
ω = 2πf = \frac{2π}{T}
\]
\[
k = \frac{F}{Δl}
\]
И в соответствии с (9)
\[
ω = \sqrt{\frac{k}{m}}
\]
\[
f = \frac{1}{2π} \sqrt{\frac{k}{m}}
\]
\[
T = 2π \sqrt{\frac{m}{k}}
\]
Масса самой пружины в (3, 4, 5) не учитывается. При точных расчетах массу m следует увеличить приблизительно на mпр/3 (mпр — масса пружины).
Величины ω, f и T не зависят от амплитуды.
\[
m = \frac{1}{3}m_{пружины} + m_{тела}
\]
Колебания пружины |
стр. 543 |
|---|
