Уравнение движения тела, брошенного под углом к горизонту, формула
Координаты точки траектории описываются уравнениями:
Здесь:
x, y — координаты тела,
u0 — начальная скорость тела (м/с),
α — угол, под которым брошено тело к горизонту (°),
g — ускорение свободного падения 9.81 (м/c2),
t — время движения (c)
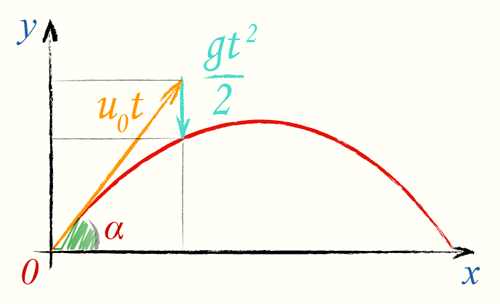
Уравнение движения тела, брошенного под углом к горизонту
Из формул 1 и 2 через параметр t выводится общее уравнение движения тела, брошенного под углом к горизонту
Так как ускорение свободного падения g, α — угол, под которым брошено тело к горизонту и начальная скорость тела u0 — постоянные величины, то координата y пропорциональна квадрату x, т.е. траектория движения представляет собой параболу, начальная точка находится на одной из ее ветвей, а вершина параболы, есть точка максимального подъема тела.
Расчитать точки траектории тела, брошенного под углом к горизонту по формуле (2)
Построить график траектории тела, брошенного под углом к горизонту по формуле (2)
Уравнение движения тела, брошенного под углом к горизонту |
стр. 417 |
|---|
