Теорема Пифагора, Теорема косинусов, Формула
Теорема косинусов, формула
Квадрат стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения одной из этих сторон на взятую на ней проекцию другой.
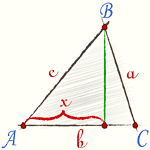 Остроугольный треугольник |
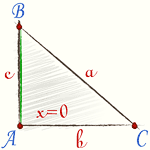 Прямоугольный треугольник |
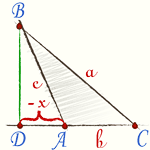 Тупоугольный треугольник |
Если угол острый то справедлива формула
\[ a^2 = b^2 + c^2 - 2bx \]
Если угол тупой то справедлива формула
\[ a^2 = b^2 + c^2 + 2bx \]
Общая формула теоремы косинусов для всех случаев треугольников выглядит следующим образом:
\[ a^2 = b^2 + c^2 - 2bc\cos(A) \]
Теорема Пифагора, Формула
Если угол прямой то справедлива формула
\[ a^2 = b^2 + c^2 \]
Квадрат гипотенузы равен сумме квадратов катетов (это Теорема Пифагора). Теорема Пифагора является частным случаем теоремы косинусов и часто применяется в разнообразных практических и теоретических вопросах.
Вычислить, найти сторону треугольника по Теореме Пифагора, Формула (4)
Теорема Пифагора, Теорема косинусов |
стр. 236 |
|---|
