Формулы и расчеты онлайн - Fxyz.ru

← Назад	Вперед →

Теорема синусов

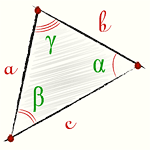
Теорема синусов гласит

Стороны треугольника пропорциональны синусам противолежащих углов

\[ \frac{a}{\sin(α)} = \frac{b}{\sin(β)} = \frac{c}{\sin(γ)} \]

Также отношение стороны треугольника к синусу противолежащего угла равно диаметру описанной окружности.

\[ \frac{a}{\sin(α)} = \frac{b}{\sin(β)} = \frac{c}{\sin(γ)} = 2R \]

Вычислить, найти сторону треугольника по теореме синусов

Пусть известно: две стороны a, b и угол между ними γ. Нужно найти сторону c и недостающие углы α и β. Используем то, что сумма углов треугольника 180°

\[ β = (180° - (α + γ)) \]

\[ \frac{a}{\sin(α)} = \frac{b}{\sin(180° - (α + γ))} \]

По формулам приведения

\[ \sin(180° - (α + γ)) = \sin(α + γ) \]

Подставим в (4)

\[ \frac{a}{\sin(α)} = \frac{b}{\sin(α + γ)} \]

по формуле синуса суммы углов разделим углы

\[ \sin(α + γ) = \sin(α)\cos(γ) + \cos(α)\sin(γ) \]

Получим

\[ \frac{b}{a} = \frac{\sin(α)\cos(γ) + \cos(α)\sin(γ)}{\sin(α)} \]

\[ \frac{b}{a} = \cos(γ) + \ctg(α)\sin(γ) \]

Отсюда найдутся все углы треугольника α и β (см. формула (3)):

\[ \ctg(α) = \frac{\Large\frac{b}{a}\normalsize - \cos(γ)}{\sin(γ)} \]

Далее теорема синусов позволит найти оставшуюся сторону c

\[ с = b\frac{\sin(γ)}{\sin(β)} = a\frac{\sin(γ)}{\sin(α)} \]

Вычислить, найти две стороны треугольника по теореме синусов

Пусть известно: одна сторона с, и два прилегающих к ней угла α и β. Нужно найти угол γ и стороны a и b. Используем то, что сумма углов треугольника 180°

\[ γ = (180° - (α + β)) \]

Теперь когда все углы треугольника известны, а также известна одна сторона, теорема синусов позволит легко найти недостающие стороны:

\[ a = c \frac{\sin(α)}{\sin(γ)} \]

\[ b = c \frac{\sin(β)}{\sin(γ)} \]

Именно так вычисляют расстояние до звезд.

Теорема синусов	стр. 238

α° (гр.)	α´ (мин)	α˝ (сек)
β° (гр.)	β´ (мин)	β˝ (сек)
c


e	π	g	C
sin	cos	tan	√	exp
asin	acos	atan	lg	ln
7	8	9	(	)
4	5	6	×	÷
1	2	3	+	-
0	.	=

Теорема синусов

Теорема синусов гласит

Вычислить, найти сторону треугольника по теореме синусов

Вычислить, найти две стороны треугольника по теореме синусов

Теорема синусов

См. также

Разделы

Калькулятор

Дополнительно