Построить график функции синус y = A·sin(x) (функция синус)
Определение синуса дано в параграфе Синус угла — sin(A).
Для построения графика тригонометрической функции синуса переменного угла по оси абсцисс задают угол в радианах, а по оси ординат какое либо число.
Линия, являющаяся графиком функции синуса, называется синусоида. При смещении графика синуса на отрезок 2·π (вправо или влево) он совмещается сам с собой.
Если график функции y = f(x) при смещении его на некоторый отрезок вдоль оси абсцисс совмещается сам с собой, то функция носит название — периодическая функция. Число p, измеряющее этот отрезок, носит название — период функции f(x).
тригонометрическая функция синуса (и вообще все тригонометрические функции), имеет период 2·π.
Для удобства экспериментов построения графиков представим x в виде линейной функции x = x(t)
Здесь ω и φ постоянные величины. φ позволяет смещать график вправо и влево. А ω позволяет сжимать или растягивать период функции. Также введем коэффициент A растягивающий функцию синуса по оси ординат.
Построение графика функции синус y = A·sin(x)
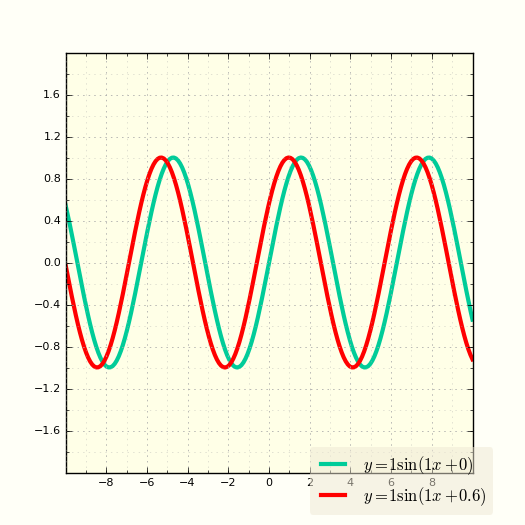
Построить график функции синус y = A·sin(x) (функция синус) |
стр. 122 |
|---|
