Построить график функции y=axn (степенная функция)
Степенная функция. Функция
(a, n — постояные величины) называется степенной. функции y=ax, y=ax2, y=a/x — частные виды степенной функции ( a=1, a=2, a=-1 )
Так как нулевая степень всякого числа, не равного нулю, есть единица, то при n=0 степенная функция становится постоянной величиной y=a. В этом случае график — прямая линия, параллельная оси абсцисс.
Остальные случаи можно разбить на две группы n>0 и n<0.
Степенная функция при n>0
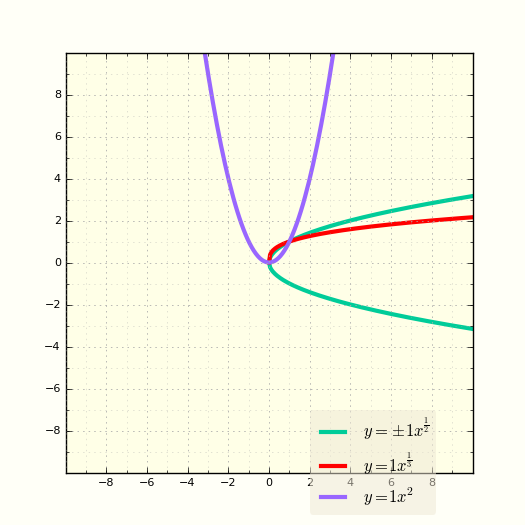
В этом случае степенная функция, ее график, проходит через начало координат и точку (1;1). Если степенная функция имеет целый показатель, то x может быть (-∞;+∞). Если степенная функция имеет дробный показатель, с четным знаменателем, то x может быть [0;+∞).
По аналогии с графиком функции y=ax2 графики всех степенных функций y=axn при положительном n назвают — Парабола n-ного порядка (или n-ной степени)
Если n=p/q с четным знаменателем q и нечетным числителем p, то величина
имеет два знака, и у графика появляется еще одна часть снизу от оси абсцисс, симметричная с верхней половиной.
Степенная функция при n<0
В этом случае степенная функция, ее график, проходит через точку (1;1). Все графики неограниченно приближаются к оси абсцисс и к оси ординат, не достигая ни той ни другой. При любом показателе степенной функции x может быть [0;+∞).
В следствии сходства с гиперболой эти графики называют — Гипербола n-ного порядка (или n-ной степени)
Построение графика функции y=axn (степенная функция)
Построить график функции y=axn (степенная функция) |
стр. 121 |
|---|
