Площадь полной поверхности правильной пирамиды через высоту, формула
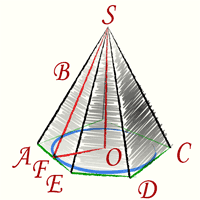
Площадь полной поверхности правильной пирамиды через высоту выводится из следующих формул
К площади боковой поверхности правильной пирамиды через высоту добавим площадь основания — площадь правильного многоугольника. Получится формула (1).
Площадь полной поверхности правильной пирамиды через высоту находится по формуле
\[ S = \frac{na}{2} \Bigg( \frac{a}{2\tg(\frac{180°}{n})} + \sqrt{ h^2 + \bigg( \frac{a}{2\tg(\frac{180°}{n})} \bigg) ^2 } \Bigg) \]
S — площадь полной поверхности правильной пирамиды через высотуn — число сторон правильного многоугольника - основания правильной пирамиды
a — сторона правильного многоугольника (AB или BC или CD или DE или EA) - основания правильной пирамиды
h — высота правильной пирамиды (OS)
Вычислить, найти площадь полной поверхности правильной пирамиды через высоту по формуле(1)
Ссылки по теме
Как найти боковую поверхность правильной усеченной пирамидыКак найти боковую поверхность правильной пирамиды
Площадь полной поверхности правильной пирамиды через высоту |
стр. 329 |
|---|
