Площадь правильного пятиугольника
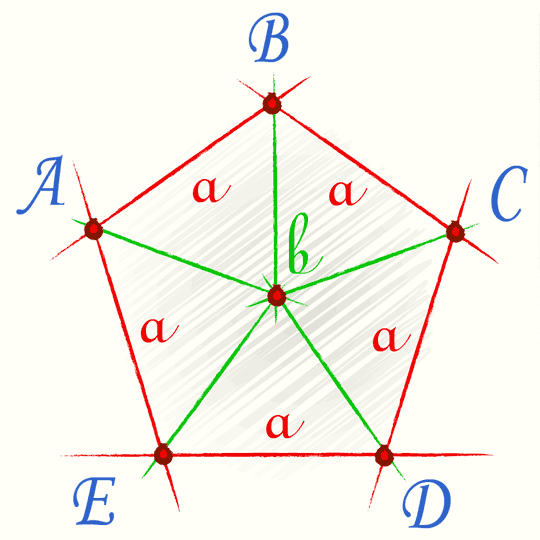
Нарисуем правильный пятиугольник.
Площадь правильного пятиугольника
Как мы видим он состоит из пяти равных равнобедренных треугольников с основанием a и бедрами b. Если мы знаем только размер стороны a правильного пятиугольника, то размер b легко находится по формуле радиуса описанной окружности правильного пятиугольника.
Таким образом получаем следующий вывод формулы:
\[ b = \frac{a}{2 \sin(π/5)} \]
\[ S_{равнобедр.треуг} = \frac{a \sqrt{b^2-\frac{a^2}{4}}}{2}\]
\[ S_{равнобедр.треуг} = \frac{1}{2} a \sqrt{\Big(\frac{a}{2 \sin(π/5)}\Big)^2-\frac{a^2}{4}}\]
\[ S = 5 S_{равнобедр.треуг} \]
\[ S = \frac{5}{2} a \sqrt{\Big(\frac{a}{2 \sin(π/5)}\Big)^2-\frac{a^2}{4}} \]
Вычислить, найти площадь правильного пятиугольника по формуле (5)
Площадь правильного пятиугольника |
стр. 321 |
|---|
