Площадь треугольника, формула Герона.
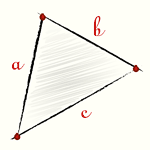Треугольник образуется соединением отрезками трех точек, не лежащих на одной прямой. При этом точки называются вершинами треугольника, а отрезки - его сторонами.
Площадь треугольника по формуле Герона равна корню из произведения разностей полупериметра треугольника (p) и каждой из его сторон (a, b, c):
\[S=\sqrt{p(p-a)(p-b)(p-c)}\]
где
\[p=\frac{1}{2}(a+b+c)\]
(a, b, c - стороны треугольника)
Вычислить, найти площадь треугольника по формуле Герона (1).
Ссылки по теме
Общая формула площади треугольникаКак найти площадь треугольника через углыКак найти площадь прямоугольного треугольникаПлощадь равнобедренного треугольникаФормула площади равностороннего треугольника
Площадь треугольника формула Герона |
стр. 302 |
|---|
